How do i compute volume of a generic hexahedron with all its faces being quadrilateral?

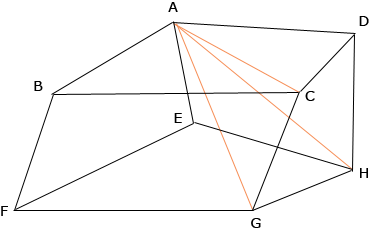
Hi,

I would compute the volume by first cutting the hexahedron into pieces.

Here is an example. In this figure I joined the point A to C, D, H and G to form a pyramid with base the quadrilateral CGHD and apex A. Remove this pyramid.

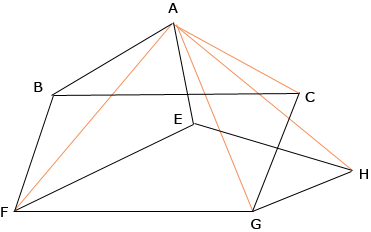
Now join A to F and remove the pyramid with quadrilateral base BFGC and apex A. Remove this pyramid.

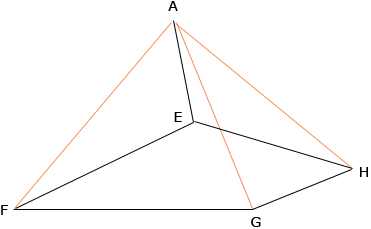
What remains is a pyramid with quadrilateral EFGH as base and apex A.

Thus I have subdivided the hexahedron into three pyramids, each with a quadrilateral as its base and hence the volume of the hexahedron is the sum of the volumes of the three pyramids.

The volume of a pyramid is ¹/₃ the area of the base the height. Each base can be divided into two triangles to find its area and hopefully you have enough information about the hexahedron to find the heights of the pyramids.

Penny