Soren,

I drew a (very crude and not to scale) diagram of what I think is the design of your birdhouse.

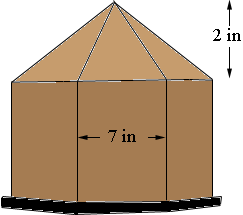
then drew a cross section showing a side and a piece of the roof. Is the angle A the angle you want?

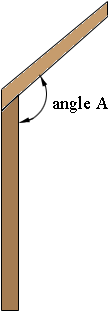
Harley

Soren wrote back.

Hello Harley -

Thank you for getting back to me so quickly. I had a feeling that I didn't articulate the question very well.

Having 'acquired' this image from another web site, assume for a moment that we're looking at one of the eight roofing sections (as the question is strictly limited to the roofing sections themselves, and not with the fit between the roof and birdhouse itself). Looking at the image, I'm thinking of the cut that needs to be made down 'side b'.

Here's what I'm thinking but I could be way off, but here goes. Assume for the purposes of discussion that the roof of the bird house is totally flat but that we're going through the exercise of making one that needs eight sections anyhow. Side b would require no angled cut down the side to allow for a tight fit because the whole thing is flat. However, as the peak of the roof rises (e.g. the center of the roof goes up), I'm assuming that an angled cut would need to be made for a tight fit so that all pieces would fit snugly together on the roof. Otherwise the depth of the pieces would align on the inside, but not outside the roof. Now I could just cut a 15-degree angle on these since the very tops would fit anyway, but now I'm curious as to how the heck to figure this out.

In short, if you add the third dimension to the drawing below that would create the thickness of the wood, I'm trying to determine what angle that thickness needs to be cut at so that the pieces fit snugly together both inside and out.

Hope that helps!!!
Soren

Hi Soren,

I think I understand now.

I used vectors to approach your problem and Mathematica to perform the calculations.

In the diagram below of the roof of the birdhouse I have drawn vectors v₁, v₂ ,v₃ and v₄ along the edges of two adjacent triangular sections.

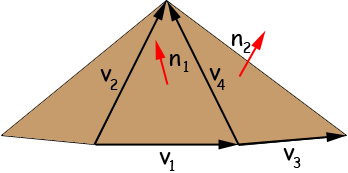
The cross product of the vectors v₁ and v₂ gives a vector n₁ which is perpendicular (normal) to the roof section containing the vectors v₁ and v₂. Likewise the cross product of the vectors v₃ and v₄ gives a vector n₂ which is perpendicular (normal) to the roof section containing the vectors v₃ and v₄. The angle between the adjacent roof sections is then the angle between the vectors n₁ and n₂ and thus the angle of the cut will be half this angle.

To find the vectors I am going to impose a coordinate system with the origin at the initial point of v₁ and v₂ , with v₁ along the x-axis, the y-axis pointing into the page and the z-axis vertical.

Here is a cross section of the birdhouse at the base of the roof. v₁ = OP and v₃ = PQ.

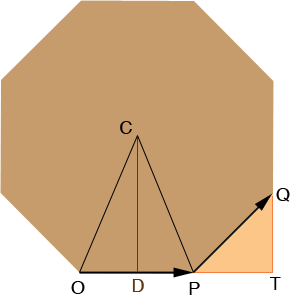
I let s be the length of a side of the octagon (the distance from O to P) and h be the height of the roof section of the birdhouse. The coordinates of O are (0,0,0) and the coordinates of P are (s,0,0). The angle PCO is 360/8 = 45 degrees or π/4 radians. (I am going to use radians for the angle measurements sinceMathematica uses radians.) The sum of the angles in a triangle is 180 degrees (π radians) and the triangle COP is isosceles, hence the angle COP is 3/8 π radians. D is the midpoint of OP and the angle ODC is a right angle and hence tan(COD) = |DC|/|OD|. Thus the y-coordinate of C is

|CD| = s/2 tan( 3/8 π).

Thus the coordinates of the point at the peak of the roof are (s/2, s/2 tan( 3/8 π), h).

Triangle QPT is a right triangle with angles QPT and TQP each measuring π/4 radians (45 degrees) and |PQ| = s and thus |PT| = |TQ| = s/√2 and hence Q has coordinates (s + s/√2, s/√2, 0).

From this information I can find the vectors I need

v₁ = (s,0,0)
v₂ = (s/2, s/2 tan( 3/8 π), h)
v₃ = (s/√2, s/√2, 0) and
v₄ = (-s/2, s/2 tan( 3/8 π), h)

This will allow me to find n₁ and n₂ .

The dot product of n₁ and n₂ is given by

n₁· n₂ = |n₁| |n₂| cos(theta)

where |n₁| is the length of n₁ , |n₂| is the length of n₂ and theta is the angle between them. Thus

cos(theta) = n₁· n₂/( |n₁| |n₂|) and theta = arccos( n₁· n₂/( |n₁| |n₂|)).

Now I am ready to use Mathematica.

Below is the output from my Mathematica session.

Cross is the cross product function, nor is a function to calculate the length of a vector in 3-space, and c2t is the cos(theta) function defined above. I then calculated this function for the values you gave, s = 7 inches and h = 4 inches. The arccos function gave an angle of 0.176516 radians which I then converted to 10.1136 degrees. Thus you need to set your saw blade to 10.1136/2 = 5 degrees.

Harley