|
 |
|
Subject: Bearings Mr. John wants to fly her airplane from point A to B, a distance of 450 miles. If B has a heading of 60 degrees from A, and there is a constant wind from the southeast blowing at 60 mph, find the speed and heading she should maintain in order to land at B in 90 minutes.
|
|
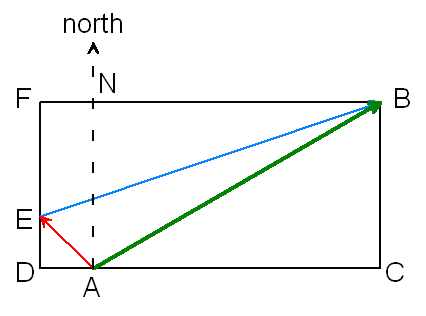
Hi Suzy. I'm a little uncertain about what "B has a heading of 60 degrees from A" means. I think the aviation convention is to measure bearings as east-positive from the North axis in the northern hemisphere (and east-positive from the south in the southern hemisphere). As I'm in the northern hemisphere, I will assume that this statement means that You want to arrive 450 miles away along this direction in 1.5 hours, so that means travelling 300 miles per hour in that direction relative to the ground. However, you have wind to consider. This makes it a vector problem.
These are velocities, not distances. The intended ground velocity is the vector in green. The wind velocity is the vector in red (it points towards the north-west because it is coming from the south-east). Therefore, you have to have an air velocity of the plane that is the blue vector. I've labelled some interesting other points to help us. Get AC: Angle NAB is 60 degrees, so angle ABC is also 60 degrees. You know the length of AB (300 mph), so you can calculate the length AC using AC = 300 sin 60. Get AD: Angle NAE is 45 degrees, so angle DEA is also 45 degrees. That means length AD is AE sin 45 = 60 sin 45. Get FB: Clearly this is just the same as AD + AC, which you just calculated. Do the same kind of thing to get BC and ED. This lets you calculate FE, because FE + ED = BC. Now you have the lengths of the legs of the right triangle FEB, so you can use inverse tangent (arctan) to find the angle FEB, which is the heading the pilot should take. And you can use the Pythagorean Theorem to find the length of EB, which is the airspeed she should fly. Hope this helps, |
 |
 |
 |