We have two responses for you, Anthony:
---

Hi Anthony,

I would set up a coordinate system with the origin at the centre of
the ferris wheel. Suppose you are at the point P(x,y) on the wheel in
the diagram.



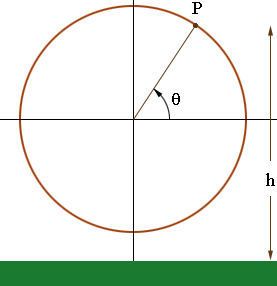
Since the diameter of the wheel is 250 feet its radius is 125 feet
and the height you are above the ground is h = y + 125 + "the
distance the base of the wheel is above the ground". From the diagram
y = 125 sin(theta) and hence all that remains in finding the height
at time t is to find theta at time t. You know that the wheel rotates
360 degrees every 40 seconds so in t seconds the wheel rotates 360/40
= 9 t degrees.
I hope this helps,

Penny

---

If you need more help, Sue gives a bit more detail:

Hi Anthony.

The path of the seat on the ferris wheel is circular.  That means that
if you were to graph the position of the seat, you could create a
circle centered at the origin.  The radius would be the radius that
the seat moves, which is 2 feet less than the radius of the ferris
wheel itself.

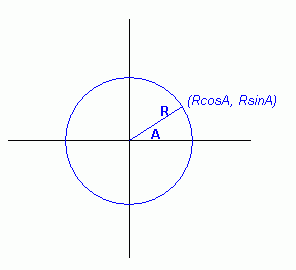
Now, the height is the y axis.  You probably already know that the
equation for the y coordinate of a R-radius circle at the origin is
(RcosA, RsinA) where A is the angle from the horizontal.  But let's
say you want to measure the angle from the bottom instead, going
clockwise.  What would be the coordinates then?  When A is 0, we want
(0, -R) and when A is 90 degrees, we want (-R, 0).  If we said
(-RsinA, -RcosA), we would have the right co-ordinates.  At 180
degrees, this is (0, R) and at 270 degrees it is (R, 0) as we hoped.

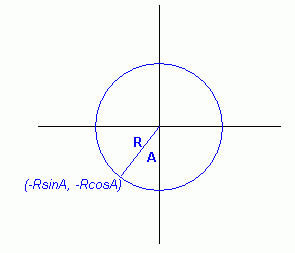
So we know the co-ordinates.  The height is the y co-ordinate: -RcosA.
Now if we draw the ground, it should be a horizontal line 4 feet below
the  bottom of the seat (because the bottom of the ferris wheel is 2
ft above the ground and the seat is 2 ft above that).

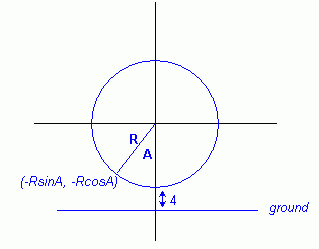
But since we want the ground to be at zero height, let's shift the
whole graph up until that horizontal ground line is on top of the x
axis.  How far did we shift it? R + 4 units up.  So really we added R
+ 4 units to the y co-ordinate which we said earlier was -RcosA.

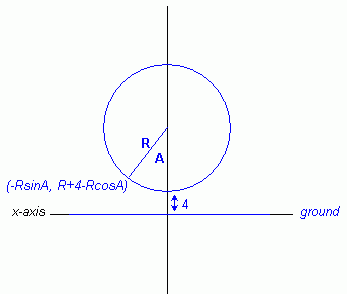
This means that the height is R + 4 - RcosA. where A is the angle from
the bottom.

Hope this helps.
Stephen La Rocque.