| |||
| Math Central | Quandaries & Queries |
|
Name: Avinash Who are you: Student Mary has 48 coins made up of nickels, dimes and quarters with a total value of $5.10. She has 4 more dimes than nickels and quarters combined. How many coins of each kind does she have? Use matrix to solve the system. |
I can get you started. Begin by assigning variable names to the unknowns:
Let N = the number of nickels,
D = the number of dimes,
Q = the number of quarters.
Then translate what you know into equations:
"Mary has 48 coins made up of nickels, dimes and quarters"
48 = N + D + Q
"with a total value of $5.10"
5.10 = 0.05N + 0.10D + 0.25Q
"She has 4 more dimes than nickels and quarters combined."
D = 4 + (N + Q)
This gives you three equations in three unknowns. You are asked to
solve it using a matrix. To do this, first re-arrange the three
equations into the form:
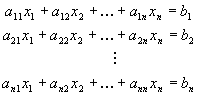
The unknowns in this general form are denoted by x1, x2, ... xn and the
coefficients (a's and b's above) are the values given. In your case,
N, D and Q would be x1 through x3.
In matrix form the system of equations above can be written as:
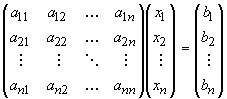
Write us back if you are uncertain about how to solve this matrix equation.
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.