Hi Joslyn,

Assuming the ocean is calm, and the boat is sitting at sea level, here is the picture we have:




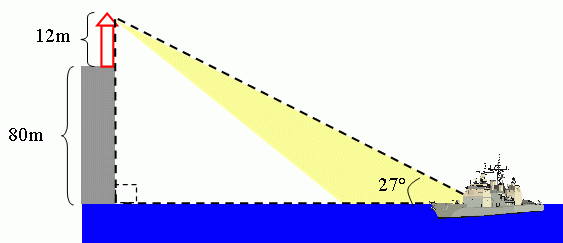
The dashed lines show you a right triangle.  We know the angle from the boat is 27 degrees. We know the length of the side opposite this angle, and we are looking for the length of the side adjacent to this angle.  What trigonometric function do you know that relates the opposite and adjacent sides of a right triangle?  Remember, tangent = opposite / adjacent.

Let x be the distance from the boat to the shore. So you have:

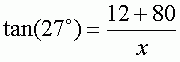
Adding the terms in the numerator, we get:

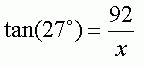
Now, we want to solve for x. So I am looking to isolate x by itself on one side of the equation. There is more than one way to do this, but just remember an equation is like a see saw. You need to keep it balanced. What ever you do to one side of the equation, you have to do to the other side, or you will unbalance it and the two sides will no longer be equal. I don't like having x in the denominator, so I'll start by multiplying both sides by x:

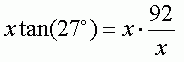
Which simplifies to:

So far so good. Now, I want to get rid of the tan(27°) on the left so that x is left by itself. I can divide both sides by tan(27°):

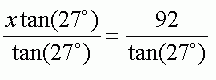
Simplifying, I get:

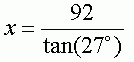
Now you can use a calculator to find an approximate value for x.

Haley