| |||
| Math Central | Quandaries & Queries |
|
Question from A, a student: A power line is to be constructed from the shore of a lake to an island that is 500 m away. The closest powerline ends 4km along the shore from the point on the shore closest to the island. If it costs 5 times as much to lay the powerline underwater as along the shore, how should the line be installed to minimize the cost? |
Hello there. Let's draw a diagram
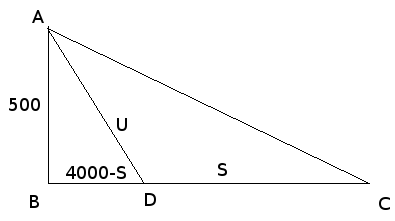
Let S = the distance along the shore and let U = the distance under water. B, C and D are points along the shoreline (I am assuming a straight shoreline!) and A is on the island.
Thus you know that the cost is C(S,U) = S + 5U. That's what you want to minimize.
To do this you need to reduce get rid of one of the variables first.
Notice that you have a right triangle. You can use Pythagoras to compute S in terms of U in terms of S:
U^2 = 5002 + (4000 - S)2
U = sqrt( 5002 + (4000 - S)2 )
Thus C(S) = S + 5 sqrt( 5002 + (4000 - S)2 )
Now you can minimize this function by taking its derivative and setting that equal to zero to solve for S.
Get in touch again if you have trouble finishing the problem.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.