We have two responses for you

Hi Adam.

The line y = x + a, where a is positive has a slope of +1 and a positive y intercept.

The slope of the circle at the point of tangency, therefore must be +1. The slope of a curve is revealed by its derivative. Where would the slope be +1? It must be either "above" or "below" the circle, but look at the diagram here:

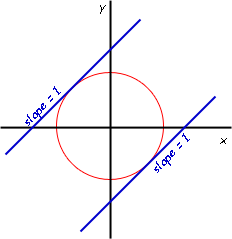
Clearly only the top line has a positive y intercept, so that is the one to look for.

Now take the derivative of the equation with respect to x:

d/dx (x² + y²) = d/dx (2)

2x + 2y dy/dx = 0

dy/dx = -x/y.

Since you know that at the point of tangency the slope is 1, we have 1 = -x / y, so y = -x.

Now let's solve for x and y knowing that they have opposite signs and the same magnitude:

x² + y² = 2

x² + x² = 2

2x² = 2

x = +/- 1.

Look again at the diagram above. Clearly, we know that the point of tangency we are interested in is in quadrant II, so we know x = -1. This means y = +1.

Now you have the point of tangency and the slope of the line, so you can quickly use the point-slope line equation to determine the line and put that into the form y = x + a to find the value of a.

Cheers,
Stephen La Rocque.

Adam,

You can solve this problem without calculus if you know that a tangent is at right angles to the radius at the point of contact. Thus the line from the centre of the circle to the point of cantact of the tangent to the circle is perpendicular to the tangent and thus has slope -1.

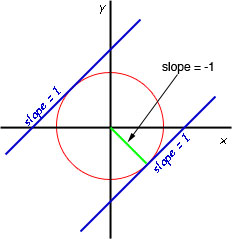
Thus the green line in the diagram passes through the origin and has slope -1 and hence its equation is y = -x. Find where this line intersects the circle and again use the point-slope line equation to determine the line and put that into the form y = x + a to find the value of a.

Harley