Two circles and a triangle

HOME

Math Central

Quandaries & Queries

Question from Adrian, a student:

The vertices of a right-angled triangle are on a circle of radius R and the sides of the triangle are tangent to another circle of radius r. If the lengths of the sides about the right angle are 16 and 30, determine the value of
R+r

Hi Adrian,

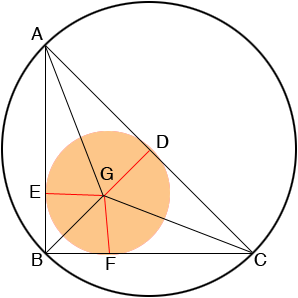
triangle and circles

Since triangle ABC is a right triangle you can use Pythagoras theorem to find the length of CA. Since the vertices of the right triangle ABC are on a circle, CA is a diameter of the circle and hence R is half the length of CA.

G is the centre of the small circle and D, E, and F are the points where the small circle is tangent to the sides of the triangle ABC.

Triangles DGC and GFC are congruent.
Triangles AGD and AEG are congruent.
Triangles GEB and GBF are congruent.

The last of these pairs of congruent triangles tell us that angles EBG and GBF are congruent and hence each measures 45 degrees. Thus |EB| = |BF| = r.

Can you complete the problem now?
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.