The rate of change of the area of a triangle

HOME

Math Central

Quandaries & Queries

Question from Ahlee, a student:

So my question is:
The included angle of the two sides of a constant equal length s of an isosceles triangle is θ.
(a) Show that the area of the triangle is given by A=1/2s^2 sinθ;
(b) If θ is increasing at the rate of 1/2 radian per minute, find the rate of change of the area when θ=pi/6 and
θ=pi/3.
(c) Explain why the rate of change of the area of a triangle is not constant even though dθ/dt is constant

Ahlee,

I can get you started.

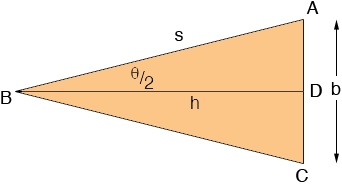
triangle

From the diagram h = s × cos(θ/2) and |AD| = b/2 = s × sin(θ/2). Thus the area of the triangle is

A = 1/2 b × h = s × sin(θ/2) ×cos(θ/2)

But the double angle formula for sin(t) is

sin(2t) = 2 sin(t) × cos(t)

and hence the area of the triangle is

A = 1/2 b × h = s × sin(θ/2) × cos(θ/2) = s/2 × sin(θ)

Now apply the calculus you know to find the relationship between dA/dt and dθ/dt.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.