Ahson,

I'm going to illustrate with f(x) = 3x⁴ - 16x³ + 24 x² - 8.

For monotonicity I need the first derivative.

f '(x) = 12 x³ - 48 x² + 48 x = 12x(x - 2)²

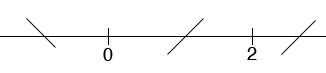
Hence the critical points are at x = 0 and x = 2. These two points separate the line into three parts and I check the monotonicity in each of the three parts.

(-∞, 0): f '(-1) < 0 and hence f(x) is decreasing
  (0, 2): f '(1) > 0 and hence f(x) is increasing
  (2, ∞): f '(3) > 0 and hence f(x) is increasing

In my rough work I usually mark this on a diagram.

For concavity I need the second derivative

f "(x) = 36 x² - 96 x + 48 = 12(3x - 2)(x - 2)

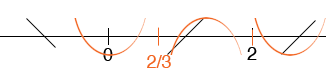
Hence the curve may change concavity at x = 2/3 and x = 2. Now I check the concavity in the 3 intervals defined by these points.

(-∞, 2/3): f "(0) > 0 and hence f(x) is concave upwards
  (2/3, 2): f "(1) < 0 and hence f(x) is concave downwards
  (2, ∞): f "(3) > 0 and hence f(x) is concave upwards

I put this information on the same diagram.

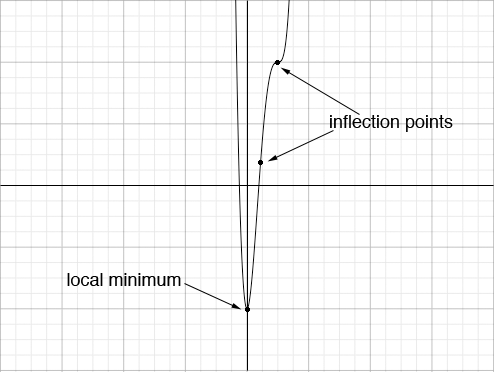
Now I'm ready to attempt a sketch but I need to plot some points to determine where on the plane the graph lies. I usually plot the critical points if this is feasible.

f(0) = -8
f(2) = 8

Here is my sketch.

I hope this helps,
Harley