Hi Alan,

The same company also makes gum drops. The weights of the gum drop packages are normally distributed with mean weight 50 g and standard deviation 0.5g. With this product only the packages weighing less than 49g are rejected. Let's find the proportion of packages that are rejected.

First, in order to use the normal probability tables you need to convert to the standard normal distribution using

Z = (X - μ)/σ

X is the random variable which is the weights of the packages of gum drops so μ = 50g and σ = 0.5 g. Thus the conversion to the standard normal distribution is

Z = (X - 50)/0.5

The proportion of packages rejected is the probability that the weight of a package is less that 49 g, that is

Pr[X < 49]

After conversion to the standard distribution this is

Pr[Z < (49 - 50)/0.5)] = Pr[Z < -2]

How you evaluate this probability depends on the form of your standard normal tab;le. My standard normal table gives me Pr(0 < Z < k) where k is a positive number. Thus from the table I can read that

Pr(0 < Z < 2) = 0.4772

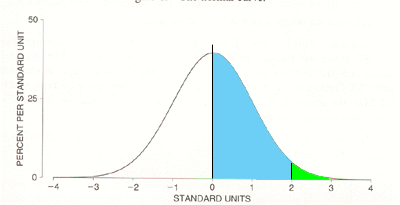
This is the area of the blue region in the diagram. Since Pr(0 < Z) = 0.5, Pr(Z > 2 ) = 0.5 - 0.4772 = 0.0228.

Finally by the symmetry of the standard normal distribution Pr(Z < -2) = Pr(Z > 2) = 0.0228. Thus the proportion of packages of gum drops that get rejected is 0.0228.

Now try the packages of sweets in your original problem,
Penny