| |||
| Math Central | Quandaries & Queries |
|
Question from Alexis, a student: Example 1. An observer is tracking a small plane flying at an altitude of 5000 ft. The plane flies directly over the observer on a horizontal path at the fixed rate of 1000 ft/min. Find the rate of change of the distance from the plane to the observer when the plane has flown 12,000 feet after passing directly over the observer. |
Alexis,
You can probably see right away that you have a right triangle. So start with some labels: y for the vertical distance above the observer, x for the horizontal distance from the observer and D for the distance along the hypotenuse.
You know that y is constant, so dy/dt is 0. You know that dx/dt is 1000 ft/min. You know that at all times, pythagoras' theorem applies, so for any particular given value of x (x = 12000 ft), you can calculate D by using Pythagoras.
As well, start with Pythagoras and differentiate both sides of the equation, using the chain rule:
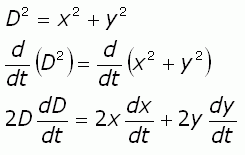
You know all these terms except dD/dt which is the rate of change of the distance between the observer and the plane, the amount you are asked to find. So solve for dD/dt, substitute in the known values and you'll have completed the problem.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.