We have two responses for you

Amar,

Draw the circle inscribed in the triangle. Then draw radii to the points of tangency. Then draw lines from the circle's center to the three corners of the triangle.

You have divided the triangle into 3 triangles and you can easily see that the height of each triangle is the radius. Since the area of the triangle is the half the height times the base, you can add the three smaller triangles' areas together to get the area of the large triangle.

Here's a diagram of what I mean:

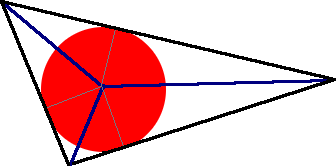
So if the sides are A, B and C and the radius is R, then the Area of the triangle is RA/2 + RB/2 + RC/2.

Can you finish the problem from here?

Cheers,
Stephen La Rocque.

Amar,

It depends on what tools you have available for 'thinking about' these connections.

(A) If you scale the entire picture down by a factor K, then both areas scale by K^2, but their ratios remain the constant. The scaling brings down the perimeters by a factor K, so their ratio remains the same. If, by chance, you are in calculus, you could look at how the areas are composed by taking limits of thin strips of the perimeters, and show that the ratio of the perimeters (A constant in all the strips) becomes the ratio of the areas when you 'add all the pieces up'.

I suspect you are not yet in calculus - though you might look for this connection, later, when you are!
This is true for other shapes than triangles! This is actually the big idea what will lie behind whatever other formulae you generate.

(B) Now how to do it 'bare handed' as it were?

First - it helps to break the triangle (and circle) down into pieces. Here is one of the six pieces I would use.

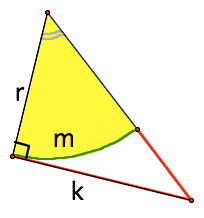
If you know about measures, you know m = r(theta) where theta is the angle In radians).
You also know that k = r cotan(theta)
But it turns out you really don't need to know any of those formula!!

The comparison you really want is the ratio of the are of the circle to the perimeter of the circle is:
(1/2) (mr)/ m = r/2. That is, for this piece: AREA C = r/2(perimeter C)

The ratio of the area of the triangle to the perimeter contributed by the triangle is: (1/2) rk /k = r/2
AREA T = r/2 (perimeter T)

Now add up over all the six pieces.
You will find the ratio of the area to to perimeter is still r/2 over both the circle and the triangle.

You can take it from there.

Walter Whiteley