| |||
| Math Central | Quandaries & Queries |
|
Question from Amit, a teacher: A rectangular sheet of a paper with dimensions a and b is folded along its diagonal. What is the area of the overlapped region? |
Amit,
I folded the sheet of paper CDBP along the diagonal CB so that P moved to A. then drew a line segment EF to meet BC in a right angle at F. Let |CA| = a, |AB| = b and then |BC| = c where c2 = a2 + b2 by Pythagoras' Theorem.
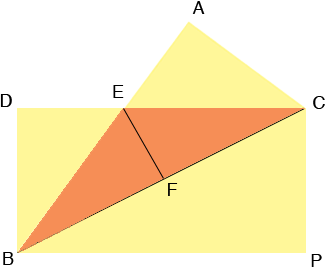
By the symmetry F is the midpoint of BC. Let |EF| = h, the height of triangle CEB.
Triangles ABC and EBF are similar.
Can you complete the problem now?
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.