We have two responses for you

Hi Amy.

Draw the diagram in quadrant one of a regular graph, with the left triangle's right angle at the origin and labelled as shown in my diagram:

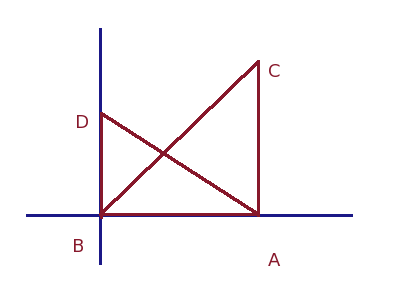
The hypotenuses (or is it hypoteni? no - that's just weird!) are line segments, so if we can find the intersection of the lines containing these hypotenuses, then we've solved the problem.

Line containing BC: y = mx + b = (180/240) x + 0 = (3/4)x
Line containing AD: y = mx + b = (-100/240) x + 100 = (-5/8)x + 100

So at the point of intersection, the (x, y) value satisfies both lines. Therefore
(3/4)x = (-5/8)x + 100.
Solve for x. Use that to solve for y.

This gives you the point of intersection. If you want to know how far this is from one of the corners (length along a hypotenuse) then you can use the distance formula to calculate it.

Cheers,
Stephen La Rocque.

Amy,

You can do it without coordinates if you wish. It's certainly not any easier but here is one way. I modified Stephen's diagram slightly to give the pont of intersection a name P.

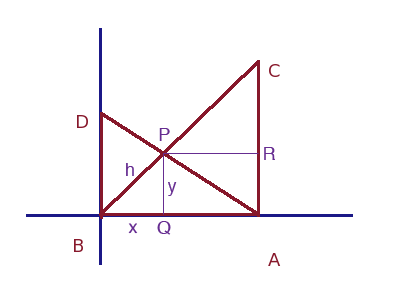
Let the length of BQ be x ft, the length of QP be y ft and the length of PB be h ft. By Pythagoras theorem

x² + y² = h²

Using pythagoras theorem on the triangle CBA I found that |CB| = 300 ft. Also |PR| = 240 - x ft,
|RC| = 180 - y ft and |CP| = 300 - h ft. Write down what Pythagoras theorem tells you for triangle PRC. Substitute x² + y² = h² into this equation and simplify. You will get a linear equation in x, y and h. Use that fact that triangles PBQ and CBA are similar to eliminate y and h and then solve for x.

Harley