Hi Andrew,

I drew a diagram of the tank to make sure we are talking about the same situation. A fact I am going to need is that the volume of a pyramid is

1/3 × the area of the base × the height.

Now I want to slice through the tank through the plane containing the red lines and look at the cross section.

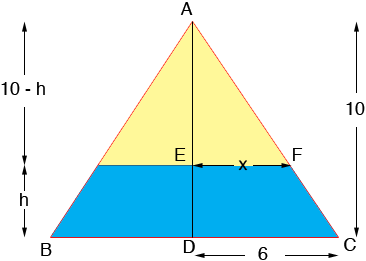
The height of the water is h feet and the top surface of the water is a square that is 2x feet on each side. Since water is flowing into the tank both h and x are functions of time. The volume V of the water in the tank is also a function of time and you know that dV/dt = 2 cu ft/min where t is in minutes. Your task is to find dh/dt at a specific time. To do this you are going to need an expression for V, the volume of water in the tank.

The volume of the tank is 1/3 12² × 10 cubic feet and hence you can find V by subtracting the volume of the empty portion of the tank, the piece shaded yellow in the diagram. This also is a pyramid and its volume is

1/3 (2x)² × (10 - h)

Hence you have an expression for V but it is a function of two variables x and h. You can use the fact that triangles ADC and AEF are similar to find a relationship between x and h and hence eliminate x from the expression for V.

I hope this helps,
Harley