Hi Andy.

Consider a regular n-gon whose sides are p units long. Let's draw two adjacent radii (length r) in red to make an isosceles triangle.

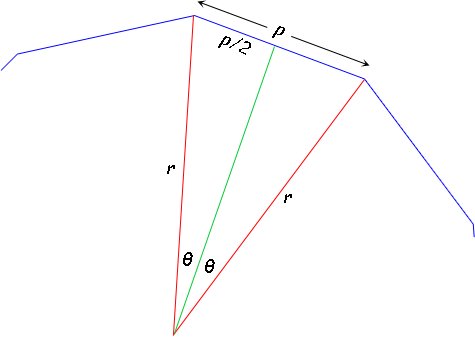
I've also drawn a line in green from the center of the polygon to the midpoint of the side. This meets the blue side in a right angle and it also bisects the central angle between the red lines. Therefore, we know that whatever the angle is between the red lines, it is divided into two equal angles I'll call theta.

Since there are n sides, there are n such red-red angles. A full circle is 360 degrees, so we are dividing it into 360/n degree isosceles triangles. This means that theta is half of that: 180/n.

Using trigonometry in the right triangle, we can use the sine relationship to discover the radius:

sin (180/n) = (p/2) / r

Solving this for r, we get

r = p / (2 sin (180/n) )

which will give you the radius corresponding to a regular polygon with n sides, each of which is p units long.

I hope this helps you. I have no idea what you mean by "array rectangles".

Cheers,
Stephen La Rocque.