Angie,

Using the notation in the diagram you sent

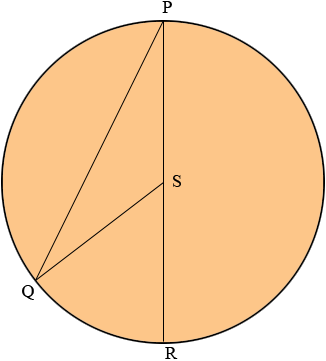
triangle PQS is isosceles and the measure of angle SPQ is 25^o so the measure of angle PQS is also 25^o. The sum of the measures of the angles in a triangle is 180^o so the measure of the angle QSP is 180^o - (25^o + 25^o) = 130^o. PSR is a line segment so the measure of the angle RSQ is 180^o - 130^o = 50^o. Can you now find the length of the minor arc QR?

If you need further assistance write back,
Harley

Angie wrote back

Harley,

Thanks for trying to help me, I actually was looking for the formula, and this was kind of confusing to me, I still can't figure out the answer, I am even more confused?

Thanks,
Angie

Angie,

I showed you that the measure of angle RSQ is 50^o. The sector RSQ is only part of the circle. The entire circle has a central angle of 360^o so sector RSQ is a fraction of the circle, in fact the sector is 50/360 = 5/36^th of the circle. The entire circumference of the circle has length 2πr where r is the radius and thus the length of the arc QR is 5/36^th of this length. Hence the length of the arc QR is

5/36 × 2πr = 5/18 πr.

Harley