An isosceles triangle inscribed in a circle

HOME

Math Central

Quandaries & Queries

Question from Anne:

Here is the math problem quoted from book:
"An isosceles triangle is inscribed in a circle of radius R,
where R is a constant. Express the area within the circle but outside
the triangle as a function of h, where h denotes the height of the triangle."

The answer from the key is A(h) = (piR^2) - (h times the square root of
(2Rh - h^2)).

I would like to know how the answer was derived, given that we only
know that R is a constant, and we know the properties of an isosceles triangle.

Thank you for the help.

Hi Anne,

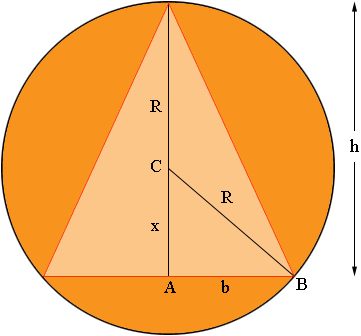
triangle in the circle

In my diagram C is the centre of the circle and x is the distance from C to A. Since the triangle is isosceles A is the midpoint of the base. let b = |AB| then b is half the length of the base of the isosceles triangle.

From the diagram h = R + x. Triangle ABC is a right triangle so using Pythagoras theorem

x² + b² = R²

Substitute x = h - R and solve for b.

The area inside the circle but outside the triangle is

π R² - bh

Substitute the value of b you found above and simplify.

Two questions:

What if the base of the triangle passes through C, that is x = 0, does the argument still work?

What if the base of the triangle is above the centre of the circle, that is x < 0, does the argument still work?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.