Hi Armando,

I can give you some suggestions and maybe help you see why you haven't found the algorithm you're looking for. This is a much more complex problem than it seems at first.

I'm going to start with the function f(x) being a polynomial and the interval an open interval (a, b) = {x | a < x < b}.

1. Find the second derivative of f(x) and call it f "(x).
   
   
2. Solve f "(x) = 0. This gives you a finite (maybe empty) set of points in the interval (a, b). If there are no points in the interval where f "(x) = 0 then there are no inflection points in (a, b). From now on assume that there are n > 0 points in (a, b) where f "(x) = 0. Call these points x₁, x₂, ... x_n and let SD be the points a= x₀, x₁, x₂, ... , x_n, x_n+1 = b where x₀ < x₁ < x₂ < ... < x_n < x_n+1. Hence I have (a, b) subdivided into n + 1 intervals. I need to refer to these intervals so I need names for them. Let I_k be the interval (x_k, x_k+1) for k = 0 to n.
   
   
3. Choose a point p_k in each interval I_k, maybe the midpoint, and evaluate f "(p_k). If the sign of f "(p_k) and f "(p_k+1) are different then f(x) has an inflection point at x_k+1.

Extensions and complications:

If the interval is a closed interval, [a, b] = {x | a ≤ x ≤ b}and say a is an inflection point of f(x) defined on the entire line do you want to call a an inflection point of f(x) defined on [a, b]?

Suppose f(x) is not a polynomial for example f(x) = x^1/3 and (a, b) = (-1, 1). x = 0 is an inflection point but f "(0) is undefined so to identify inflection points where the second derivative is undefined you have to include is SD all points in (a, b) where f "(x) is undefined.

Suppose f(x) = sin(1/x) and (a, b) = (0, 1). f "(x) exists for each x in (0, 1) and there are infinitely many places where f "(x) = 0. f(x) = sin(1/x) has infinitely may inflection points in (0, 1).

I hope this gives you an idea of the complexity of your question.

Harley

Armando wrote back

Hello. I recently sent a question about how to calculate inflexion points given an arbitrary equation, which was already answered on the site (greatly appreciated). Unfortunately, I failed at explaining the problem at the first time, so here I send a much more detailed description of the real problem I’m facing, hoping you can figure it out once more.

What I’m really trying to do is to solve a given equation in a specific range (or interval). In other words, find the roots of the equation. (Screenshots are from the very same program I’m developing):

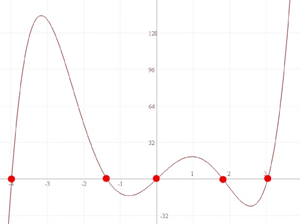I’d like to find the x-coordinate of the red-marked points, they are the roots of the function:  x5 + 1/2 x4 - 15 x3 + 3 x2 + 30 x - y = 0 When y = 0. (This is just an example; it’s not that I want to find these specific roots.)

Depending on the type of equation it might have any number of roots. I could use directly a method for finding the roots such as the Newton method (or the bisection method, it doesn’t really matter), the problem is that I haven’t found a method that returns ALL of the roots in the specified range.

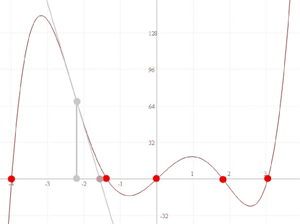Depending on the initial guess, Newton’s method (which is the one I’d like to use), for example, will converge (if it does) to only one of the roots. Instead I’d like to find all of the roots.

One way to solve this out (I guess) is splitting the range into sub-ranges in such a way that every sub-range will end up with no more than one root. Then I could use the Newton’s method on every sub-range, which will return the output I want. Now the problem is: how do I define these sub-ranges?

Please notice that I’d like my software to do all of the math, no third party components. Otherwise it would be too easy and I wouldn’t learn the hard part (I found writing math-related programs a great and entertaining way of studying math, precisely by struggling with situations like this).

Again, if you could lend me a hand out of this endless loop it will be a great help.
Thankfully,
Armando.

Hi again Armando,

I shortened somewhat what you sent because I want to talk about your original goal which is to find all the zeros of a given function in a specific range. I agree with you that this is great way of studying mathematics.

Your example function is a polynomial and I am going to stick to polynomials because it illustrates a place where the theory is neat and clean but in practice there are some real difficulties. The theory I want to look at is

Polynomial Factor Theorem
If a polynomial p(x) has a root r, that is p(r) = 0 then (x - r) is a factor of p(x).

This means that if p(x) = 0 then there is a polynomial q(x) so that p(x) = (x - r) q(x). Thus if you have a root r you can divide p(x) by (x - r) to obtain q(x) and then look for roots of q(x). The polynomial q(x) is of smaller degree than p(x). This looks like it solves your problem. Find a root r, divide by (x - r) to obtain q(x) and start again, this tie with the polynomial q(x). Continue until the polynomial is a quadratic and then find the final 2 roots using the standard method.

The difficulty arises because you don't have a root, you have an approximation from Newton's method and the division process to find q(x) has accumulated round off error. It would be interesting to try it with your software and the example you gave above, p(x) =  x⁵ + 1/2 x⁴ - 15 x³ + 3 x² + 30 x. You know one root is x = 0 and division of p(x) by (x - 0) = x yields q(x) =  x⁴ + 1/2 x³ - 15 x² + 3 x + 30. Use Newton's method to find an approximate root r and then divide q(x) by (x - r). You should get a zero remainder. Do you? Do the division by hand and see how many times you use the approximate root r. Every time you use r you accumulate the round off error inherent in r.

I want to mention another theoretical result that might be a help. One of the challenges in what you are attempting to do is that you don't know how many roots the polynomial has. There is a result that may help

Descarte's Rule of Signs
If the terms of a single-variable polynomial with real coefficients are ordered by descending variable exponent, then the number of positive roots of the polynomial is either equal to the number of sign differences between consecutive nonzero coefficients, or less than it by a multiple of 2.

For your polynomial p(x) =  x⁵ + 1/2 x⁴ - 15 x³ + 3 x² + 30 x there are two sign changes so p(x) has at most 2 positive roots. Now substitute x = -x and the polynomial becomes p(-x) =  -x⁵ + 1/2 x⁴ + 15 x³ + 3 x² - 30 x. Apply Descarte's Rule and again there are 2 sign changes so the original polynomial p(x) has at most 2 negative roots. You can easily see that p(x) has a root at x = 0.

Lets look at another example s(x) = x³ + x² + 1. Descarte's Rule Of Signs tells me that this polynomial has no positive roots and at most 1 negative root.

I hope my comments are of some use to you. Keep up the good work,
Harley