| |||
| Math Central | Quandaries & Queries |
|
Question from astrogirl, a student: find the volume of the biggest right circular cone that can be inscribed in a sphere of radius a=3 |
Hi,
In my diagram the sphere has centre C and radius R. The cone has base radius r and height h.
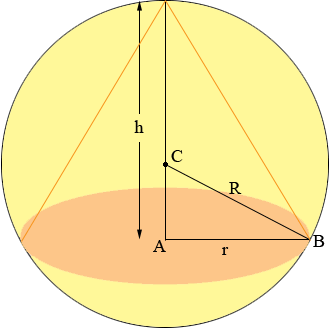
The volume of a right circular cone is V = 1/3 π r2 h. To apply the calculus you know you need to express this volume as a function of one variable. The right triangle ABC give the information you need.
By Pythagoras theorem
|CA|2 + |AB|2 = |BC2|
thus
(h - R)2 + r2 = R2
or
r2 = R2 - (h - R)2
Substitute r2 into the expression for the volume of the cone and you have then a function of one variable h. Use your calculus to find the value of h that maximized the volume.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.