Subdividing a chord - Math Central

Math Central

Quandaries & Queries

Here is my question. Imagine I have a circle of known radius 25 feet, and a chord with a mid point height of 6 inches from a central point on the chord to the circumference of the circle. I wish to divide this chord into a number of equal divisions. How can I calculate the measurement of the perpendicular line at each division of the chord to the circumference and at a 90 degrees at each division

Austin,

The equation of a circle with its centre at the origin is x² + y² = r² where r is the radius. For your problem I think it will be more convenient to work in inches rather than feet so the equation of the circle is

x² + y² = (25 × 12)² = 300² = 90,000

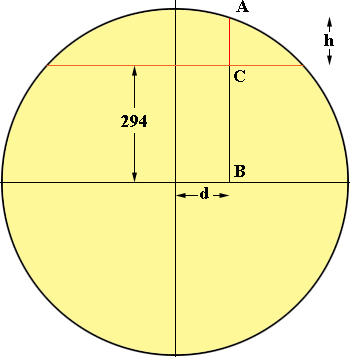
circle

Suppose you move d inches away from the midpoint of the chord. You want the height h in the diagram. Since the equation of the circle is

x² + y² = 90,000

we have

d² + y² = 90,000

where y is the length of the line segment AB. Since the length of BC is 300 = 6 = 294 inches

d² + (294 + h)² = 90,000
(294 + h)² = 90,000 - d²

h = √(90,000 - d²) - 294 inches.

Thus, for example if d = 1 ft = 12 inches then

h = √(90,000 - 12²) - 294 = √(90,000 - 144) - 294 = √(89856) - 294 = 299.76 - 294 = 5.76 inches

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.