| |||
| Math Central | Quandaries & Queries |
|
Question from Awrongo, a student: A long time ago Mr Gibson found an island shaped as a triangle with three straight shores of length 3 km,4 km and 5 km. He declared an 'exclusion zone' around his island and forbade anyone to come within 1 km of his shore. What was the area of his exclusion zone? |
We have two responses for you
Awrongo,
What do you know about a triangle which has sides lengths in the ratio of 3 to 4 to 5?
The exclusion zone can be seen as composed of 6 pieces. Three are rectangular pieces, each 1 km wide and with lengths 3km, 4km, and 5 km. The other three pieces are sectors of circles of radius 1 km.
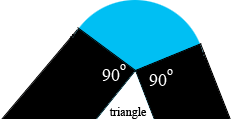
Can you see how to use you knowledge of the 3 by 4 by 5 triangle to find the area of each sector?
If you need more help write back,
Penny
Hi Awrongo.
The sum of the interior angles of a triangle are 180 degrees. That means the sum of the exterior angles is 3x360 - 180 = 900 degrees. If you subtract the 90 degree "straight" parts (2 per corner), then you have 900 - [3 x 2 x 90] = 900 - 540 = 360 degrees. That's a full circle. So the curved area is π square kilometers.
Thus the exclusion zone is 1 x (3+4+5) + π = 12 + π square kilometers.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.