| |||
| Math Central | Quandaries & Queries |
|
Question from Barbara, a student: If the base of a larger triangle is 34 inches long, what is the length of side A of the smaller triangle? (the small triangle has on top the letter a on the right side of the triangle it has the letter b, and at the bottom of the small triangle it has the number 17) Thank you |
Hi Barbara,
I am not sure I have the diagram correct but here is my interpretation of what you sent. The large triangle is PST and the small triangle is PQR.
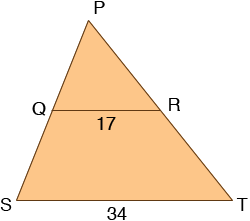
If QR is parallel to ST then the triangles PQR and PST are similar. This means, in particular, that the ratios of the lengths of the corresponding sides is the same. that is
(length PQ)/(length PS) = (length QR)/(length ST) = (length RP)/(length TP)
Since (length QR)/(length ST) = 17/34 = 1/2 you can conclude that PQ is half as long as PS and RP is half as long as TP.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.