Hi Becc,

You can draw the triangle if you wish.

Draw a line segment of length 3.1 cm and label the endpoints a and b. Set the point of a compass at a and with a radius of 4 cm draw an arc of a circle.

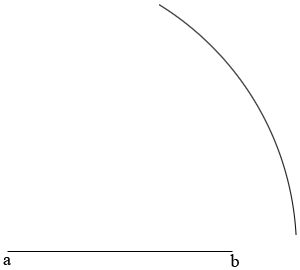
Move the compass point to b and draw an arc of radius 2 cm draw another arc. Call the intersection of the arcs c. Complete the triangle abc.

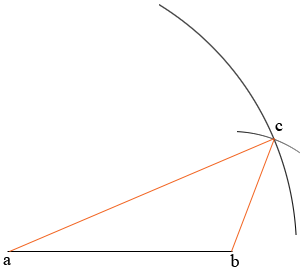
You can now measure the height.

The value you obtain for h depends on the accuracy with which you can measure, both the measurement of h and the measurements in the construction. A better way to find the height is to use algebra.

Draw a triangle and label it abc. Draw a line from c, perpendicular to ab to meet ab at d. |CD| = is the height of the triangle. Let |ad| = x.

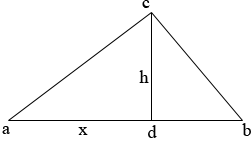
(In the construction I found that the triangle is obtuse but that's not how I drew the triangle above. The calculations will show that abc is obtuse.)

Triangles adc and dbc are right triangles so using Pythagoras theorem

|ac|² = h² + x²

and

|bc|² = h² + |db|²

Substituting your numbers

4² = h² + x²

and

2² = h² + (3.1 - x)²

Solve these equations for x and then substitute the value for x into 4² = h² + x² to find h. When you do this you will see that x is larger than |ab| = 3.1 cm so d is to the right of b and the triangle is obtuse.

Penny