| |||
| Math Central | Quandaries & Queries |
|
Question from bob, a parent: So, I'm making a chart to help me mix watercolor paints. There are 25 different paints. Each paint will mix with another paint just 1 time. There is no need to mix red with blue, and then blue with red. Since the result is the same, we only need 1 combination of the 2 paints. And there is no need to mix red with red, so we can eliminate 25 combinations of the same paint. |
Hi Bob,
I would set up an array of colour chips much as you see a mileage chart on some maps. Here is an example with only 5 colours.
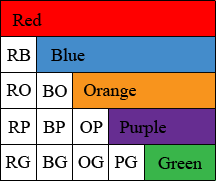
The pairs of letters identify the colours being mixed, BP for blue and purple, OG for orange and green for example.
How many colour chips will it take? In your case you could form a 25 by 25 square with all the pairs of colours, GO as well as OG and also GG and OO. That would be 25 × 25 = 625 squares. As you noted you don't need the diagonal entries which are a colour mixed with itself. There are 25 squares on the diagonal so that leaves 625 - 25 = 600. But you only need half of these, only the square below the diagonal, so you are left with 600/2 = 300 colour chips. In my example the calculation is (5 × 5 - 5)/2 = 10.
This seems a strange thing to do as I expect mixing watercolours is much more complex. What if you mix one part orange with 3 parts green? How much water do you use?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.