A five-sided coin - Math Central

HOME

Math Central

Quandaries & Queries

Hello there,

I have been grappling with this problem from Abbott and Neil's "Teach Yourself Trigonometry" for a few days now
and it is driving me bananas!

I really would like to get the solution to the following problem:
A new five-sided coin is to be made in the shape of figure 8.6
The point A on the circumference of the coin is the centre of arc CD, which has a radius of 2cm
Similarly B is the centre of arc DE, and so on.
Find the area of one face of the coin.
I cannot get it. Answer should 3.03sqcm, but I cannot understand how this result was arrived at.
The exercise is in the chapter on Radians and should not involve any complex calculations.

I would be most grateful if someone would post a solution to this problem!!!

Thanks

Carla

Hi Carla,

I added four lines to your diagram to complete the regular pentagon ABCDE.

coin

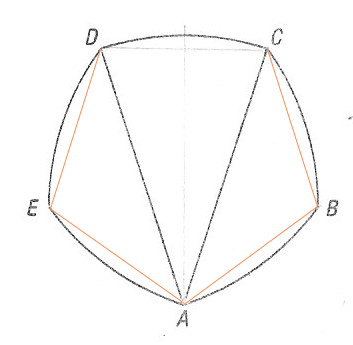
Since ABCDE is a regular pentagon the measure of the angle ABC is π - 2π/5 = 3π/5 radians. Triangle ABC is isosceles and hence the measure of the angle BCA is (π - 3π/5)/2 = π/5 radians. The measure of the angle BCD is 3π/5 radians so the measure of the angle ACD is 3π/5 - π/5 = 2π/5 radians. Triangle CDA is also isosceles and hence the measure of angle DAC is π - 2 × 2π/5 = π/5 radians.

Is this enough to get you started?

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.