The angle between two faces of a pyramid

HOME

Math Central

Quandaries & Queries

Question from Carla, a student:

A pyramid has its vertex directly above the centre of its square base.
The edges of the base are each 6cm, and the vertical height is 8cm.
Find the angle between 2 adjacent slant faces.

I would be ashamed to say how much time I spent trying to figure out this one...

Thanks.

Carla

Hi Carla,

I used vectors to solve this problem. First put a coordinate system on 3-space with one of the vertices of the base of the pyramid at the origin O and two of the sides of the base lying on the X and Y axes as in the diagram.

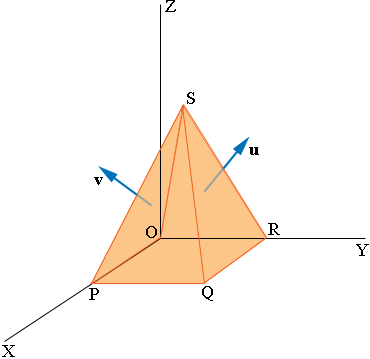
pyramid

P has coordinates (6, 0, 0), R has coordinates (0, 6, 0) and S has coordinates (3, 3, 8). The vector cross product OS × OR gives a vector u which is perpendicular to the triangular face SOR. The vector cross product OP × OS gives a vector v which is perpendicular to the triangular face SPO. The angle between u and v is angle between the faces SOR and SPO. Use the vector dot product of u and v to find the angle between them.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.