We have two responses for you

Hi Carla,

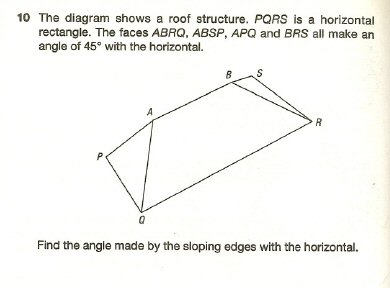
Let's say the height of the peak is h units.

Picture dropping a vertical line through the attic to its floor and connect that point as point X. You can also draw a line from A to the midpoint of PQ (I'll call that point Y).

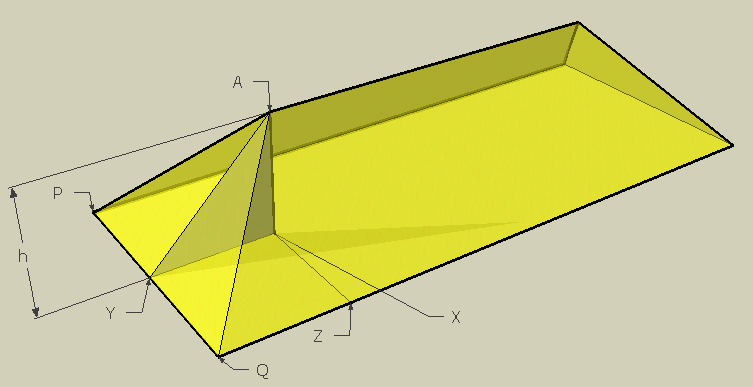
Now since angle AXY is a right angle and angle AYX is 45 degrees, then angle XAY is also 45 degrees. This is a 45-45-90 triangle. So since we said length of AX (the height) is h units, then the length of XY is also h units because it is an isosceles triangle. In fact, from symmetry, I think you can recognize that YQZX is a square with side length h.

Consider the right triangle AXY. Pythagoras then tells us that the hypotenuse AY is sqrt(2) times h. (AY² = h² + h²)

Next look at triangle AYQ. It is also a right triangle. You should easily be able to find the hypotenuse length AQ, now that you know AY and YQ.

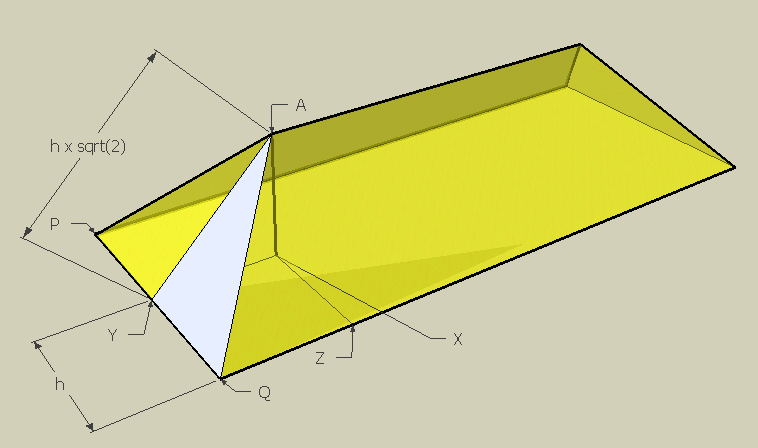
Finally, I'll draw the line XQ. See the inside triangle AXQ?

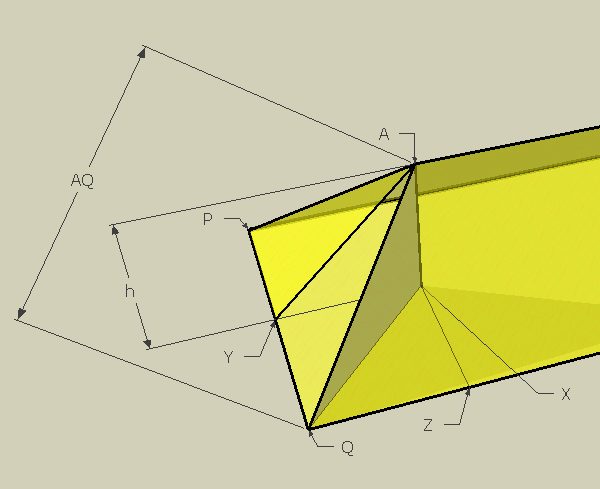
It's a right triangle as well. The height AX is still h units. You found the length of AQ. You want the measure of angle AQX.

For that, you can use the trig function sine, because AQ is the hypotenuse, and AX is the opposite side in the right triangle AXQ. Actually, you need to use arcsine (inverse sine) to find it.

sin(θ) = AX / AQ

Can you finish the problem now?

Cheers,
Stephen La Rocque.

Carla,

This question is asking whether we should use vectors, to which my answer is NO.

You can assume without loss of generality that the roof is a pyramid with a square base. Because of the equal angles, the sides of the base each equal twice the height. Following Steve's notation, call the top of the pyramid A, the center of the square base X, and one of the corners of the square base Q. Then AX = 1, XQ = √2, and hence the measure of angle AQX is arctan (1/√2).

Chris