| |||
| Math Central | Quandaries & Queries |
|
Question from Carolyn, a student: I am doing construction. I have a line segment drawn. I need to divide a segment into 3 congruent part. How do I do that? |
Carolyn,
The key is in similarities, in particular similar triangles.
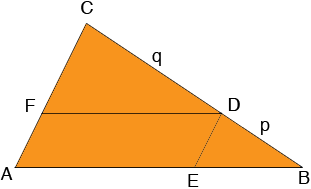
Start with a triangle ABC and a point D on BC so that the ratio of the lengths of BD to DC is p to q, in your case take p = 1 and q = 2. Construct a line through D parallel to CA and meeting AB at E. Construct a line through D parallel to AB and meeting CA at F. AEDF is a parallelogram and hence AE and DF are congruent.
The triangles CFD and DEB are similar (do you see why?) and hence
|EB|/|FD| = |BD|/|DC| = p/q
Does this help?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.