Hi Charles,

I drew an end view of the tank and converted all the measurements to inches.

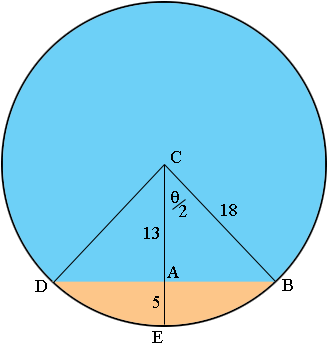
The volume of fuel in the tank is the area of the region shaded orange times the length of the tank which is 72 inches. The area of the orange region is the area of the sector CDB minus the area of the triangle CDB. To determine these areas I need the length of AB and the measure of the angle BCD which I am calling θ, in radians.

Triangle CDB

The triangle ABC is a right triangle and thus by Pythagoras theorem |AB| = √(18² - 13²) = 12.45 inches. Thus the area of the triangle CDB is 12.45 × 13 = 161.85 square inches.

Sector CDB

The area of the sector CDB is 1/2 r² θ where r is the radius of the circle and θ is the angle BCD measured in radians. From the diagram cos(θ/2) = 13/18 and hence θ = 2 cos^-1(13/18) = 1.53 radians and hence the area of the sector CDB is 1/2 × 18² × 1.25 = 247.47 square inches.

The area of the orange region is thus 247.47 - 161.85 = 85.97 square inches.

The volume of fuel in the tank is thus 85.97 × 72 = 6189.61 cubic inches. There are 231 cubic inches in a US gallon so 6189.61 cubic inches is 6189.61/231 = 26.79 gallons.

I hope this helps,
Penny