| |||
| Math Central | Quandaries & Queries |
|
Question from Christy, a student: This question is similar to the previous one I asked before. A calculus question, I have no idea how to start though. A rectangular plot of farmland will be bounded on one side by a river and on the other three sides by a single-strand electric fence. With 800m of wire at your disposal, what is the largest area you can enclose, and what are its dimensions? |
Christy,
I would start with a diagram. Since the question is about the area of a rectangle and the area is given by the length times the width I would label the length and width, for example with L and W.
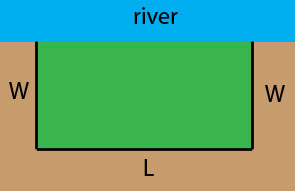
You want to maximize the area which is given by A = L × W. This is a function of two variables L and W and you need to express it as a function of one variable to apply the calculus you know to maximize the area. The fact that will allow you to do this is that the length of wire available is 800m. From the diagram you need fencing along the length and the two sides and hence L + 2W = 800.
Use this fact to express the area as a function of one variable and then you can use calculus to finish the problem.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.