Hi Claudette,

This is a particle moving along a line and its distance from the origin is given by x(t) = sin²(2t) for t between 0 and 2. It would be nice if units were given but they are not so I will say distance units. I drew a graph of x(t) = sin²(2t)

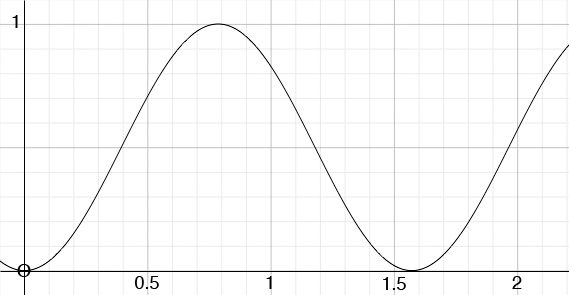
x(t) = sin²(2t)

The height of this function tells you the distance the particle is from the origin, so for example when t = 0.5 the particle is approximately 0.7 distance units from the origin.

The particle starts at a distance of 0 units from the origin at t = 0 and moves away from the origin attaining a distance of 1 unit at t approximately 0.8. It then moves back toward the origin and reaches the origin when t is a little larges than 1.5. Thus as t moves from 0 to 1.5 the particle moves 1 unit from the origin and then returns to the origin, thus traveling 1 + 1 = 2 distance units.

Looking at the graph above you can see that the point again moves away from the origin until t = 2. When t = 2, x(t) = x(2) = sin²(4). Thus in total the point have moved 2 + sin²(4) distance units.

I hope this helps,
Harley

Claudette responded

In his answer, Harley has drawn a graph that shows sin²(2t) in action. However, helpful as that is, the author of the problem has stated that the distance is 2.57. Obviously it is helpful to see the graph, but this problem calls for a specific decimal measurement.

Is it possible, given the information by this author, to actually compute 2.57 in a mathematical sense WITHOUT a graph being drawn. I suppose also, it is a bit confusing when I see sin²(2t). What is the difference in a graph between sin²(2t) and sin(2t)?

Another question for clarification sake.

At the conclusion to the problem, the answer is expressed by the author as 2 + sin²(4) Why is the notation sin²(4) an ADDITION to the 2. I am assuming that the Sin²(4) somehow is equivalent to .57, since the author of the problem states that the answer is 2.57. How do we determine that sin²(4) is equal to .57, since the final answer is 2 + sin²(4)?

Warm Regards,
Claudette

Hi again Claudette,

The notation sin²(2t) means (sin(2t))². Something that is important to see in this problem is that the variable 2t is measured in radians not degrees. I used my calculator to find sin(4) and got sin(4) = -0.7568. (If you do this make sure your calculator is set to radians.) Thus

sin²(4) = (sin(4))² = (-0.7568)² = 0.57

Thus the answer in decimal form is

2 + sin²(4) = 2 + 0.57 = 2.57

I plotted sin(2x) and sin²(2x) on the same graph o that you can see how they compare

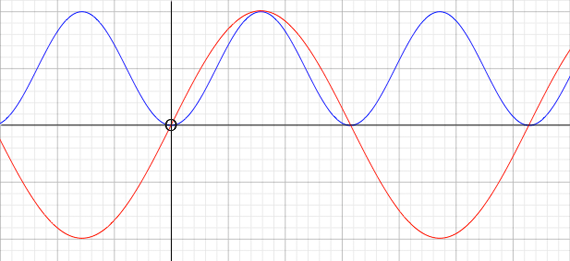
sin(2x) and sin²(2x)

You certainly can solve this problem without a graph of the function but you need a general idea of its shape. The arch in the sin²(2t) function to the right of the origin says that the particle moves away from the origin a distance of 1 distance unit and then returns to the origin going a total of 2 distance units. It then moves away from the origin a distance of sin²(4) = 0.57 distance units.

I hope this helps,
Harley

Dear Harley:

Thanks again!

My problem is that if we look at the graph, the frequency seems to be the same for sin^2 (2A) and sin (2a) If that is true, I don't see how the distance traveled by the particle can be different in the same amount of time.

Stated differently, the graph confuses the issue for me.

The extreme of both values is still "1" and the time is the same. If the frequencies are the same as well, I don't really have a clue in terms of doing the problem mathematically.

How we can translate sin²(4) as .57 is simply a mystery. Stated differently, how can sin²(4) be .57? What is the formula for that? How do we show mathematically (not using the graph at all) that sin²(4) equals .57.

And further WITHOUT benefit of the graph, how can we say that the answer here is 2 + sin²(4)?

All I am really seeing is the particle reaching is maximum and minimum on the graph a couple of times, and then at the end having a bit left over which is labeled as .57.

If my life depended on it, I wouldn't be able without the graph to even come close to telling
anyone why sin²(4) would have such a value.

For example, when we calculate a derivative for an equation such as x⁵ + x⁴ + x³ we have a process that is clear. The derivative would be x⁴ + x³, etc When calculating a distance on a straight line we can use the distance formula. Here, all I am seeing is a graph with nothing to support it with a formula or process. We are just being told that the answer is 2+ Sin²(4), check it out on the graph.

What am I missing, Harley? You seem so confident. I am sure you are seeing a lot more than I am here.

Had I a graphics calculator, I would not have a problem doing the graph, but leaving that out of the picture (no pun) how can I do this with pencil and paper.

What is the formulaic process, Harley?

I am feeling very slow indeed!

Warm Regards,

Claudette

Claudette,

"How do we show mathematically (not using the graph at all)" Mathematicians have been doing geometry and using diagrams for thousands of years. To somehow suggest that using the graph is not mathematics is ignoring thousands of years of history. Trying to do mathematics whiling ignoring geometry is like learning to play the piano but insisting on only using your left hand. Mathematics is so much more than using formulas.

There is a great deal of information in the graph.

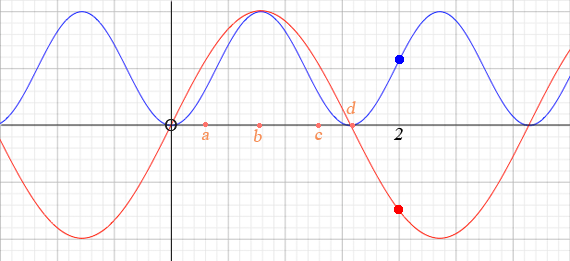
At time zero I am in my red car at a stop light and beside me is a red car. We are both facing east. When the light turns green the red car starts away much more quickly than I do. At the time labeled a on the diagram The red car is further from the light than I am. One unit distance from the light, at point b, we both do a u-turn. I navigate the u-turn better than the red car and when we come out of the turn I am closer to the stop light than the red car at point c. I have to slow down at the light and make another u-turn while the red car continues west. At the time when t = 2 our positions are shown by the dots on the graphs. This is more information than you need to solve the problem but you said "I don't see how the distance traveled by the particle can be different in the same amount of time."

How do you solve the problem without a graphing calculator? You need to recognize that sin²(2t) is zero at t = 0, 1 at 2t = π/2 and the zero again at 2t = π or t = π/2 which is approximately t = 3/2 = 1.5. Thus in approximately 1.5 time units the particle has gone from 0 to 1 and back to zero for a total of 2 distance units. sin²(2t) is again 1 at 2t = 3π/2 or t = 3π/4 which is larger than 2 so t = 2 before the particle is again 1 distance unit from the origin. In fact at time t = 2 the distance from the origin is sin²(2 × 2) = sin²(4).

This is the one place where I need to use a calculator. I make sure my calculator is in radian measure and evaluate sin(4). I obtain sin(4) = -0.7568. But I want sin²(4) = (sin(4))² = (-0.7568)² = 0.57 distance units. Thus in the time from t = 0 to t = 2 the particle has gone 2 + 0.57 = 2.57 distance units.

Harley