Hi Dave,

A hexadecagon is a 16 sided polygon. I have also seen it called a hexadecagon or a hexakaidecagon. I assume you mean a regular hexadecagon, one where all the sides are the same length and all the interior angles are equal in size. If you join each vertex of a regular hexadecagon to the centre you partition the figure into 16 congruent triangles. Three of them are in my diagram below and one is labeled as triangle ABC. I also let w be the width of the hexadecagon.

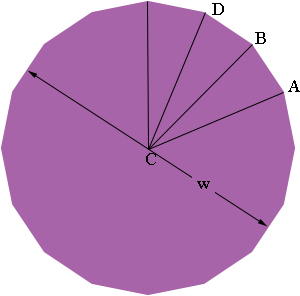
Since the 16 triangles are congruent angle BCA = 360^o/16 = 22.5^o. Since the triangle ABC is isosceles angles ABC and CAB are congruent. Thus angle ABC = (180^o - 22.5^o)/2 = 78.75^o and angle ABD = 2 × 78.75^o = 157.5^o.

The length s you cut each side, for example s = |AB|, depends on how large you want the hexadecagon to be. Look at triangle ABC again.

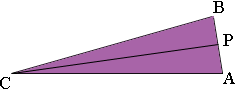
If P is the midpoint of AB then |PB| = s/2, |CP| = w/2 and angle BCP = 22.5^o/2 = 11.25^o. Hence

tan(11.25^o) = |PB|/|CP| = s/w

and thus

s = 0.1989 w

I hope this helps,
Penny

In December of 2013 we received this question note Felly

I have read the post above, but I don't understand how the .1989 number is calculated. I would like to employ the same math for a 20 sided polygon, the tangent being 9 degrees instead of 11.25, so I assume the multiplier would change accordingly? Thx!

Hi Felly,

In a right angled triangle such as triangle $BPC$ above if you select one of the non-right angles, such as angle $BCP$ then the tangent of this angle is the length of the opposite side divided by the length of the adjacent side. Thus in the example above

\[\tan\left(BCP\right) = \frac{|BP|}{|CP|}\]

or

\[\tan\left(11.25^o\right) = \frac{s}{w}\]

and thus

\[s = w \times \tan\left(11.25^o\right)\]

What remains is to find the value of $\tan\left(11.25^o\right).$ For this I used my calculator. I input 11.25 and then pressed the button labeled tan. My calculator returned 0.1989...

You need to take care that your calculator is in degree mode. To make sure calculate $\tan\left(11.25^o\right).$ If you get 0.1989 then you can proceed with your angle. If you don't get 0.1989 your calculator is probably in radian mode and you need to switch it to degree mode.

Write back if you need more assistance,
Penny