| |||
| Math Central | Quandaries & Queries |
|
Question from David, a student: Direction: Identify the open intervals on which the function is increasing or decreasing. f(x)=1/(x^2) i understand how to get up until there, and the undf. is x=0, but now i'm having problem setting up the number table chart. i cant remember how, and where to place the increase and decrease + - the |
Hi David,
I agree with your solution so far. There in no x for which f '(x) = 0 but there is one x for which f '(x) is undefined, that is x = 0. At this point I draw a sketch of the line and mark every place where the derivative is zero or undefined.
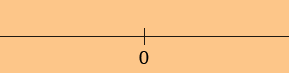
The points marked on the line are the only places where the derivative can change sign. These points divide the line into intervals, in your case (-∞, 0) and (0, ∞).
One at a time take a point in each interval and find f ' at that point. I am going to take x = 1 in (0, ∞). f '(1) = -2/13 = -2 and hence f(x) is decreasing at x = 1. Since x = 0 is the only place where f ' can change sign, f(x) is decreasing at every x in (0, ∞). I mark this on the sketch by
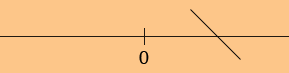
Next take a point in (-∞, 0), I took x = -1. This time f '(-1) = -2/(-1)3 = 2 and hence f(x) is increasing for x in (-∞, 0), and again I put this information on the diagram.
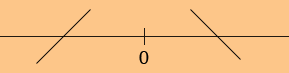
Finally I can read off the diagram that f(x) is increasing for x in (-∞, 0) and decreasing for x in (0, ∞).
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.