| |||
| Math Central | Quandaries & Queries |
|
Question from Don, a parent: Thank you for such a great site. Unfortunately the depth of my math skills leaves me unable to figure out this question. I am trying to determine the length of an arch with a two foot backset from 32 foot frontage. The answer to this question will permit us to carry on with the construction of our veterans memorial wall. Thank You Don |
Hi Don,
Here is how I am interpreting your question. Please let me know if my interpretation is incorrect.
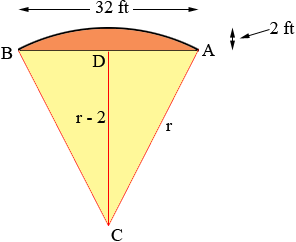
You have a 32 foot frontage, (A to B in my diagram) and a circular arc from A to B that is backset 2 feet at the midpoint of the frontage, D in my diagram. I let C be the centre of the circle and called its radius r feet. ADC is a right triangle with |AD| = 16 feet and |DC| = r - 2 feet and hence using Pythagoras theorem
r2 = (r - 2)2 + 162 = r2 - 4r + 4 + 256
Thus
4r = 260
and hence
r = 65 feet.
If the angle BCA is measured in radians then the length of the arc from A to B is
arclength = r × angle BCA
I can find the angle DCA which is half of the angle BCA because tan(DCA) = |AD|/|DC| = 16/63 = 0.2540. Thus angle DCA = tan-1(0.2540) = 0.2487 radians and angle BCA = 2 × 0.2487 = 0.4974 radians. Hence
arclength = r × angle BCA = 65 × 0.4974 = 32.33 feet.
Harley
In August 2009 Don sent us these photos of the veterans memorial wall



 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.