Overbooking flights - Math Central

HOME

Math Central

Quandaries & Queries

Question from DON, a student:

Overbooking by Airlines

This is a simplified version of calculations used by airlines when they overbook
flights. They realize that a certain percentage of ticketed passengers will cancel
at the last minute. Therefore, to avoid empty seats, they sell more tickets than
there are seats, hoping that just about the right number of passengers show up.
We will assume that the no-show rate is five percent.
For a flight with 220 seats, the airline wants to find how sensitive various
probabilities are to the number of tickets it issues. In particular, it wants to
calculate
a) the probability that more than 225 passengers show up
b) the probability that more than 220 passengers show up
c) the probability that at least 215 seats will be filled
d) the probability that at least 210 seats will be filled.
To assess the benefits and drawbacks of issuing various numbers of tickets on an
airline flight with 220 seats, create a table showing as many different scenarios
as possible (table only on one page when printed) and use a second page for
your analysis and recommendation to the airline. Which are the good cases,
which are the bad cases for the airline?

Hi Don,
Since there is a failure to show up rate of 5% and we want a full plane,
0.95x=220
x=231.57
since the number of passengers is a whole number, we will take the maximum seats the airline will book is 231 (usually best to round down in situations like this).

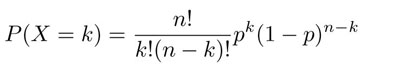
conomial distribution

This is a binomial distribution problem, finding the probability of success or failure. In general, the probability of getting exactly k successes in n trials is given by the probability mass function:
where p is the probability if success (0.95), 1-p is the probability if failure (0.05), k is the successes or maximum number of seats booked (231 seats) and n is the number if trials (more than 225 passengers from part a). Remember we need to include all the probabilities that are greater than 225 to the maximum which is 231

conomial distribution

There are about a 2.4% chance that more than 225 passengers will show up. You can solve the other parts of the question using the same method.
Janice

For further help with binomial distributions check out: http://mathcentral.uregina.ca/QQ/database/QQ.09.05/belinda1.html

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.