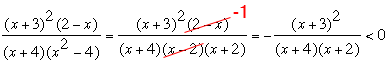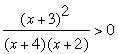Hi Ed,

What I notice first is the difference of squares x² - 4 = (x - 2)(x + 2) in the denominator and (2 - x) in the numerator so I am going to have some cancellation.

You know that this cancellation is invalid if x - 2 = 0, that is x = 2 so when you are done you nee to check that x can't be 2.

Now multiple each side by -1 which changes the direction of the inequality and leaves us with

Now I see that (x + 3)² can't be negative so I can divide both sides by (x + 3)² to obtain

Again this step is invalid if x = -3 and in fact x = -3 does not satisfy the original inequality so you need to insure when you report the final result that x = -3 is not given as a solution.

If the inequality above is true then either both (x + 4) and (x + 2) are positive or they are both negative. Can you complete the problem now?

If you need more assistance write back,
Penny