The elevation of the sun

HOME

Math Central

Quandaries & Queries

Question from Elena, a student:

Please help!! i have no idea at all where to even start!

The "angle of elevation" of an object about you is the angle between a horizontal line of sight between you and the object. (See figure) After the sun rises, its angle of elevation increases rapidly at first, then more slowly, reaching a maximum near noontime. Then the angle decreases until sunset. The next day the phenomenon repeats itself. Assume that when the sun is up, its angle of elevation (E) varies sinusoidally with the time of day. Let t be the number of hours that has elapsed since midnight last night. Assume that the amplitude of this sinusoid is 60 degrees, and the maximum angle of elevation occurs at 12:45 p.m.. Assume that at this time of year the sinusoidal axis is at E=-5 degrees. The period is, of course, 24 hours.

a. Sketch a graph of this function
b. What is the real-world significance of the t - intercepts?
c. What is the real world significance of the portion of the sinusoid, which is below the t-axis?
d. Predict the angle of elevation at 9:27 a.m., and at 2:30 p.m..
e. Predict the time of sunrise
f. As you know, the maximum angle of elevation increases and decreases with the change of the seasons. Also, the times of sunrise and sunset change with the seasons. What one change could you make to your mathematical model that would allow you to use it for predicting the angle of elevation of the sun at time on any day of the year.

Hi Elena,

I would start by sketching a piece of the sine function without axes since the axes described in the question are not in the conventional place. The horizontal units are hours t and the vertical units are degrees of the angle of elevation E. One thing you do know is that the amplitude is 60 degrees.

sine

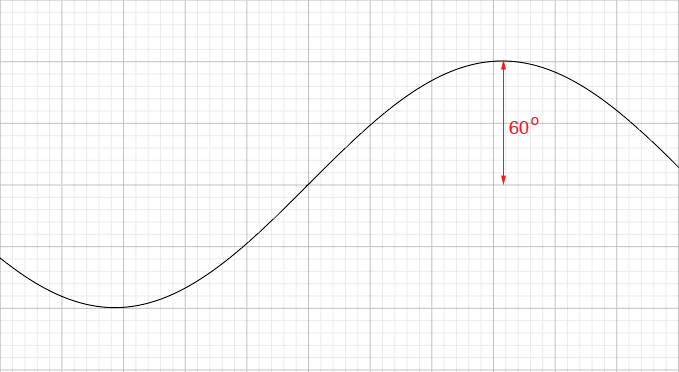
You are told that "the sinusoidal axis is at E=-5 degrees" so the horizontal axis is 5 degrees below the conventional x-axis.

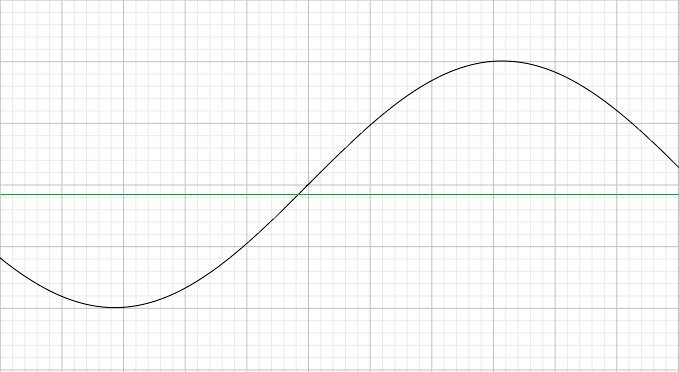
x-axis

The maximum elevation is at 12:45 p.m., 45 minutes after noon and the period is 24 hours so the minimum elevation is 12 hours earlier at 12:45 a.m., 45 minutes after midnight. Since t is the number of hours that has elapsed since midnight the vertical axis must cross the horizontal axis at midnight which is 45 minutes (3/4 of an hour) before the minimum elevation.

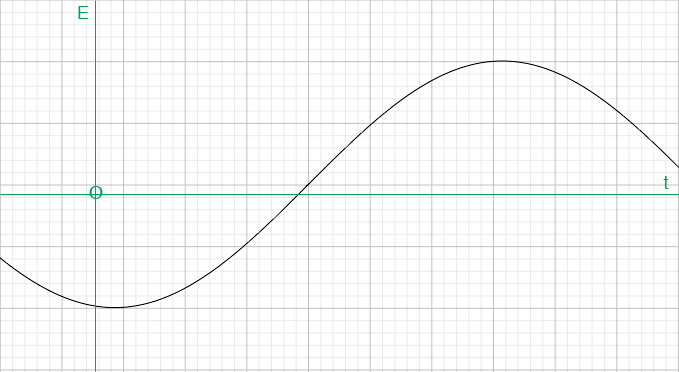
y-axis

Does this help?
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.