We have two responses for you

Elisha,

The important fact here is that rate = distance/time or in other words distance = time × rate.

Suppose the train from England travels at e km/h then the train from France travels at e + 8 km/h. Suppose also that the train from England travels d km in 17 minutes. Since the trains meet at this time the train from France must travel 50 - d km in 17 minutes. In this description I used time in hours at one point and time in minutes at another. I need to use the same units in both places and I decided to use hours so I will use 17 minutes = 17/60 hours.

From distance = time × rate for the train from England I get

d = 17/60 × e

Write a similar expression for the train from France. This gives you two equations in d and e. Solve for e.

Penny

Hi Elisha,

Since we do not know where the trains pass each other, we will choose an arbitrary point:

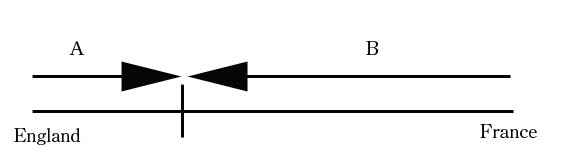
The distance from England to the passing point is A and the distance from France to the passing point is B. If we let the velocity of the train traveling from England be v then the train traveling from France will be v+8. Remember that since our speed is in km/h, we need to have consistent units so time=17/60 hour. We know A +B=50km and distance = velocity x time so

(17/60)v +(17/60)(v+8)=50

Now solve for v and you will have the speed of the train traveling from England.