| |||
| Math Central | Quandaries & Queries |
|
Question from GEORGE, a teacher: Statistics texts state that in a normal distribution, 1 standard deviation covers 68%, 2SD 95% 3SD 99.7%. However, on looking at the tables for normal curve areas, the percentage for a z value of 1 is 84.13. 68 % of values are covered at a z value of 0.47. The discrepancies exist even for other values but are smaller. So why is the rule of thumb so different from the Table for Normal Curve areas? |
Hi George,
When I look up a z value of 1 in my table of standard normal table I get the value of Pr(0 < z < 1) as in the diagram below, and the value in the table is 0.3413, or if you prefer 34.13%.
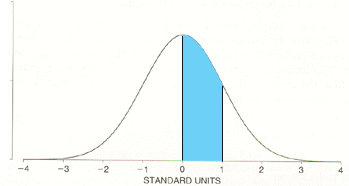
Pr(0 < z < 1)
It looks like you have added 50% to this value to obtain 84.13%. That would give you Pr( z < 1).
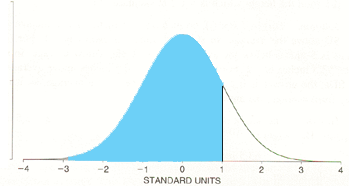
Pr( z < 1)
When the statistics texts state that "in a normal distribution, 1 standard deviation covers 68%" they mean that 68% of the probability (area) is between -1 and 1.
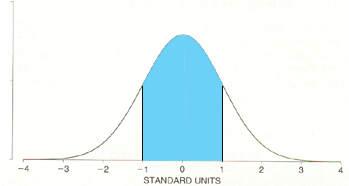
Pr(-1 < z < 1)
To find the value of Pr(-1 < z < 1) from the table you need to double the value of Pr(0 < z < 1). Hence the value is 2 × 0.3413 = 0.6826 or approximately 68%.
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.