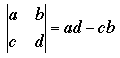| |||
| Math Central | Quandaries & Queries |
|
Question from Henry: I have a question about solving 3x3 matrices. The traditional way, or at least the way I've been taught, is that if one has a 3x3 matrix such as: [ a b c ] one solves it according to this formula: [ei - hf) - (bi - hc) + (bf - ec) = determinant. According to a book I'm now studying to prepare for the California CSET exam, there is another, easier, way to solve it: [ a b c ] [ a b ] In other words, one repeats the first two rows of the matrix and adds them to the right. At this point, the determinant is calculated thus: (aei) +(bfg) + (cdh) - (gec) - (hfa) - (idb). Is this, in fact, correct? Henry |
Hi Henry,
Two by two determinants are easy
You can evaluate a 3 by 3 determinant by expanding down the first column. You first form three 2 by 2 determinants by first stroking out the first row and first column
: determinant = ei - hf
next stroking out the second row and first column
: determinant = bi - hc
and finally stroking out the third row and first column
: determinant = bf - ec
The determinant of the 3 by 3 matrix is formed from these three 2 by 2 determinants as
= a(ei - hf) - d(bi - hc) + g(bf - ec)
This is what you have as the value of the determinant except that you forgot the leading a, d and g.
The determinant can also be evaluated by expanding down the second column or down the third column, or in fact across the first, second or third rows. You need only be careful of the signs of the leading coefficients. For example, expanding across the second row gives
= -d(bi - hc) + e(ai - gc) - f(ah - gb)
One of the advantages of this technique is that it extends to larger determinants. For example you can evaluate a 4 by 4 determinant by expanding down the first column and evaluating the four resulting 3 by 3 determinants.
The second method you give for evaluating a 3 by 3 determinant is valid but it has a serious flaw. The method doesn't extend to larger determinants.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.