We have two responses for you

Hello James. The best way to go about a problem like this is to create a diagram of what you are actually trying to figure out. So you are starting with a circle

Then we have a circle inside of this circle and since the size of the smaller circle can change we will give this circle a radius r.

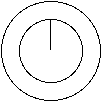
Now the toughest part is placing the chord. It says that the chord rests on top of the smaller circle so we can place it anywhere.

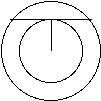
A theorem in geometry is that if a chord touches the edge of a circle it creates a right angle with the radius of that circle.

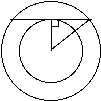
Then from here we can use the Pythagorean Theorem to help us find the radius of the big circle. Since the length of the chord is 100, half of that would be 50 and this would be one of the legs of the right triangle, then the radius r would be the length of the other leg of the right triangle. So your equation for the radius R of the larger circle can be figured out using the Pythagorean Theorem and looks like the following equation R² = r² + 50². Thus i you know the radius r of the smaller circle you can find the radius R of the larger circles radius you then can use A= π R² o find the area of the larger circle.

Hope this helps.

Brennan Yaremko

Hi James.

You don't have enough information to find the area of either circle,
because there are several scenarios that fit your description.

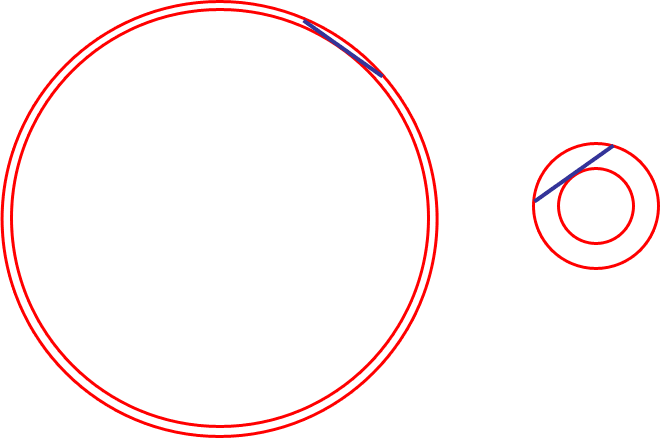
In both cases, I have created two concentric circles with a 100 pixel long chord of the larger which is tangent to the inner circle. I think you will agree that the circles could be any co-ordinated size.

Here is an interesting thing, though (and perhaps this is what you meant to ask): The area between the
concentric circles is the same in both cases!

The reason for this is due to Pythagoras.

Due to symmetry, the chord is tangent to the inner circle at its midpoint. So if we label the radii as R and r, we get this:

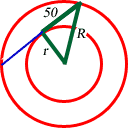
Can you finish the problem and calculate the area of the ring between the circles?

Cheers,
Stephen La Rocque.