Hi James,

y = 3x - 5x² = x(3 - 5x) crosses the x-axis at x = 0 and x = 5/3 so find the area of the region bounded by y = 3x - 5x² and the x-axis by integrating 3x - 5x² from x = 0 to x = 5/3. Call the value A.

Suppose the line through the prigin y = mx intersects the parabola at Q with x-coordinate p.

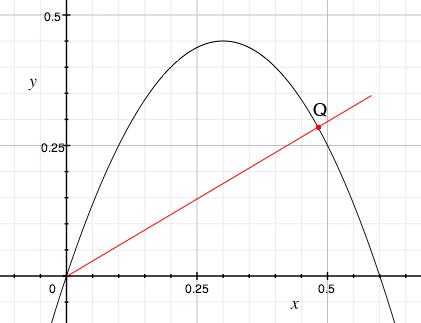
The task is to find m so that

Evaluation of the integral gave me

1/2 (3 -m) p² - 5/3 p³ = A/2                             (1)

The relationship between p and m comes from the fact that the point Q is on the line y = mx and also on the parabola y = 3x - 5x². Thus mp = 3p - 5p² or p = (3 - m)/5. Substitute into (1) to get

1/2 (3 - m) (3 - m)²/25 -5/3 (3 - m)³/125 = A/2

Solve for m.

Harley