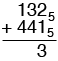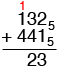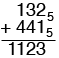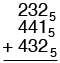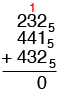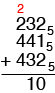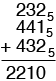Hi Jana,

I'm glad you found Stephen's note on counting in different bases helpful.

One thing you need to keep in mind when working in base five is that the only digits you have are 0, 1, 2, 3 and 4. The other digits we work with, like 6 and 9 are just meaningless squiggles when working in base five. In what I am going to do I will only write digits 0, 1, 2, 3 and 4 except in one place. I will write a subscript of 5 on some numbers to remind us that we are working in base five but the subscript 5 is not part of the number. So let's add 132₅ and 441₅.

Add the units column. 2 + 1 = 3.

Now add the second column. 3 plus 4 is seven. (Notice that I don't write the meaningless squiggle 7.) Seven is 12₅ so , just as in adding in base 10, I write down the 2 and carry the 1.

Finally add the third column. 4 plus 1 is five plus the carry of 1 gives six. Six is 11₅ so I get

Hence 132₅ + 441₅ = 1123₅

Now let's try three base five numbers.

The sum of the units column is five. Five is 10₅ so write down the 0 and carry the 1.

The sum of the second column, including the carry is eleven. Eleven is 21₅ so write down the 1 and carry the 2.

Finally, the sum of the last column, including the carry is twelve. Twelve is 22₅ and hence

Thus 232₅ + 441₅ + 432₅ = 2210₅

Now try a multiplication yourself. Write down a base 5 multiplication problem just as you would if it were in base 10. Proceed as if you were working in base 10 but remember to convert all the numbers to base 5 before you write them down.

Write back if you need further help,
Harley