Hi Jason,

I always draw a diagram. Here the diagram is a right triangle. One leg is of length 12 inches and I don't know the length of the hypotenuse so I called it h inches. The other leg then has length h - 3 inches.

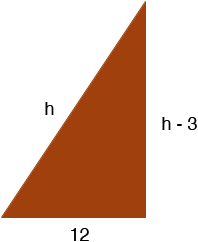
What does Pythagoras' theorem tell you?

Penny

Jason wrote back

Question from Jason, a student:

Thanks, for replying so fast. One leg of a triangle is 12 inches long. The other is 3 inches shorter than the hypotenuse. Find the length of the hypotenuse. I guess, I should have told you my steps for solving this
problem the first time I asked the question. I know how to set up the problem but I just don't know what to do next after I squared h-3. I know that I can use the pythagorean theorem to find the length of the
hypotenuse, which is a square + b square=c square. The problem here is that I only know the length of one of the legs. This is how I set up the problem: 12 square + (h-3)square = h square. Then, I get 144 + h square -6h + 9 = h square. After that, I don't know what to do next, do the h squares cancel themselves? and then solve for h. If I do that, I get h=25.5, is that the hypotenuse? or do I have to subtract 3 from 25.5 and then solve 12 square + 22.5 square = h square.

Jason,

What you did is correct. Once you have

144 + h² - 6h + 9 = h²

you can subtract h² from each side to get

144 + h² - 6h + 9 - h² = h² - h²

which simplifies to

144 - 6h + 9 = 0

giving h = 25 ¹/₂

Penny