Perimeter, area and diagonals of a rectangle

HOME

Math Central

Quandaries & Queries

Question from jenea, a student:

I have to find the perimeter as well as the area of a rectangle when given the diagonals are 12 units long and they intersect at a 60 degree angle. how do i find both the area and perimeter; do i use the 30 60 90 triangle rule?

We have two responses for you

Hi Jenea,

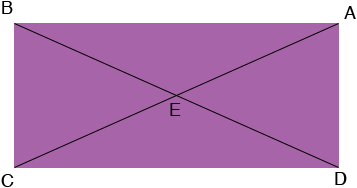
rectangle

It looks like triangles ABE and CDE are similar. Can you prove it? (Actually they are congruent but similarity is enough.) If they are similar then |AB|/|CD| = |BE|/|DE|. But |AB| = |CD| and hence |BE| = |DE| = 6 units.

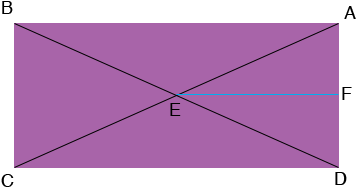
rectangle

The measure of angle AED is 60 degrees and EF bisects this angle so triangle FED so if you can show that the measure of angle DFE is 90 degrees then triangle FED is a 30 60 90 triangle and you can use what you know about such triangles to find the lengths of DF and FE.

Once you have the lengths of the rectangle sides CD and DA you can check your answer by using Pythagoras theorem to verify that the length of the diagonal is 12 units.

I hope this helps,
Penny

Steve has a nicer solution than mine. Penny

Jenea,

In Penny's diagram BE = CE by symmetry, so triangle EBC is isosceles. If mCEB = 60, then triangle EBC is equilateral, so that means that the right triangles formed by using a diagonal, are 30 60 90 triangles.

The relationship of the side lengths and the hypotenuse (the diagonal) in a 30 60 90 triangle are always the same. You should know what that relationship is so you can just "scale" to make the hypotenuse 12 units long and you will see the length of the sides which let you answer the question.

Stephen La Rocque

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.