A multiple choice exam - Math Central

HOME

Math Central

Quandaries & Queries

Question from jon, a student:

a student is taking a multiple choice exam in which each question has four choices.
assuming that she has no knowledge of the correct answers to any of the questions, she
has decided on a strategy in which she will place four balls (marked A, B, C, D) into a box. she randomly
selects one ball for each question and replaced the ball in the box. the marking will determine her answer to the question.
there are five multiple choice questions on the exam. what's the probability that she will

(a) get five questions correct
(b) at least four questions correct
(c) at most three questions correct
(d) no questions correct
(e) what are the mean and standard deviations she will get correct in (a)

thanks for your help

Hi Jon,

I would use a tree diagram to approach this problem. I drew a tree diagram but for an exam with only three questions.

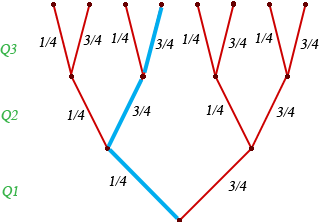
tree diag

For each question the probability that she gets the correct answer is 1/4 and the probability she gets an incorrect answer is 3/4. I have highlighted one possible result in blue. It is the result that she got the first question correct and the second and third questions incorrect. The probability of this result is 1/4 × 3/4 × 3/4 = 1/4 × (3/4)². If you examine the tree diagram you will see that there are 3 results with exactly one question correct and hence the probability that she gets exactly one question correct is 3 × 1/4 × (3/4)².

This analysis leads you to the binomial distribution. That is

The probability that she gets exactly n question out of 3 correct is
3! / ( n! (3-n)! ) × (1/4)ⁿ × (3/4)^3-n.

Now try this for an exam with 5 questions.

Harley and Stephen

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.