How many bricks I can place around a 26-inch circle?

HOME

Math Central

Quandaries & Queries

Question from Jon:

I want to know how many bricks I can place around a 26-inch circle? There must be a formula other than trial and error. The length of the bricks is 6-inches. [How many 6-inch tangents can be in a 26-inch circle?
Thank you very much.
Jon

Hi Jon,

Here is a piece of an n-sided regular polygon with an inscribed circle of radius r units and centre C.

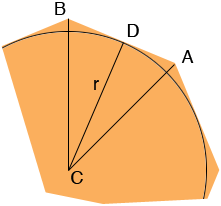
polygon

Since the polygon has n sides the measure of the angle BAC is 360/n degrees. Thus the measure of the angle DCA is 180/n degrees. If the length of the side AB of the polygon is s units then the length of AD is s/2 and

tan(180/n) = (s/2)/r = s/(2r)

Hence

tan^-1(s/(2r)) = 180/n

and

n = 180/tan^-1(s/(2r))

You have s = 6 inches and r = 26/2 = 13 inches so

n = 180/tan^-1(s/(2r)) = n = 180/tan^-1(6/26)= 180/12.9946 = 13.85

So 14 bricks should be sufficient.

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.